Naive Bayes

Introduction

The Naive Bayes classifier is included in the e1071 package. We will also load the MLmetrics and ROCR packages in order to use their functions for evaluation caclulations and ROC curves.

library(e1071)
library(MLmetrics)
library(ROCR)

For this example we are going to use the Breast Cancer Wisconsin (Original) Data Set. The steps for loading and splitting the dataset to training and validation are the same as in the decision trees notes

Training

Next we construct the classifier.

model <- naiveBayes(Class ~ ., data=trainData)
print(model)

## 
## Naive Bayes Classifier for Discrete Predictors
## 
## Call:
## naiveBayes.default(x = X, y = Y, laplace = laplace)
## 
## A-priori probabilities:
## Y
##    benign malignant 
## 0.6634981 0.3365019 
## 
## Conditional probabilities:
##            ClumpThickness
## Y               [,1]     [,2]
##   benign    2.971347 1.669291
##   malignant 7.197740 2.474965
## 
##            UniformityCellSize
## Y               [,1]      [,2]
##   benign    1.277937 0.8235752
##   malignant 6.649718 2.6610431
## 
##            UniformityCellShape
## Y               [,1]      [,2]
##   benign    1.406877 0.9532514
##   malignant 6.711864 2.5297155
## 
##            MarginalAdhesion
## Y               [,1]      [,2]
##   benign    1.340974 0.9773646
##   malignant 5.559322 3.1941238
## 
##            SingleEpithelialCellSize
## Y               [,1]      [,2]
##   benign    2.063037 0.7889561
##   malignant 5.350282 2.3958801
## 
##            BareNuclei
## Y               [,1]     [,2]
##   benign    1.318584 1.191182
##   malignant 7.657143 3.112294
## 
##            BlandChromatin
## Y               [,1]     [,2]
##   benign    2.108883 1.077276
##   malignant 6.045198 2.313054
## 
##            NormalNucleoli
## Y               [,1]      [,2]
##   benign    1.237822 0.9211137
##   malignant 5.774011 3.3734933
## 
##            Mitoses
## Y               [,1]      [,2]
##   benign    1.037249 0.2760339
##   malignant 2.632768 2.5351281

The result includes the following components:

apriori: Class distribution for the dependent variable.
tables: A list of tables, one for each predictor variable. For each categorical variable a table giving, for each attribute level, the conditional probabilities given the target class. For each numeric variable, a table giving, for each target class, mean and standard deviation of the (sub-)variable.

In our case because we have numeric attributes the mean and standard deviations are shown.

Prediction

Given the model we start making predictions

predict(model, validationData)

##   [1] benign    benign    malignant malignant benign    benign    benign   
##   [8] malignant malignant malignant malignant malignant malignant malignant
##  [15] malignant malignant malignant benign    malignant benign    benign   
##  [22] malignant benign    malignant benign    benign    benign    benign   
##  [29] benign    malignant malignant benign    benign    benign    benign   
##  [36] benign    malignant malignant benign    malignant benign    malignant
##  [43] malignant benign    benign    malignant benign    benign    benign   
##  [50] benign    benign    malignant malignant malignant malignant malignant
##  [57] benign    malignant benign    benign    malignant malignant benign   
##  [64] malignant benign    malignant benign    malignant benign    benign   
##  [71] malignant malignant malignant benign    malignant benign    malignant
##  [78] benign    malignant benign    benign    malignant benign    benign   
##  [85] malignant malignant malignant malignant malignant malignant benign   
##  [92] benign    benign    benign    malignant benign    malignant benign   
##  [99] benign    malignant malignant malignant benign    benign    malignant
## [106] benign    benign    benign    malignant malignant benign    benign   
## [113] benign    benign    benign    benign    malignant benign    benign   
## [120] benign    benign    malignant benign    benign    benign    benign   
## [127] benign    benign    malignant benign    malignant malignant benign   
## [134] benign    benign    malignant benign    benign    malignant benign   
## [141] malignant malignant malignant benign    benign    benign    benign   
## [148] malignant benign    malignant benign    benign    malignant benign   
## [155] benign    benign    benign    benign    benign    benign    benign   
## [162] benign    benign    malignant benign    benign    benign    benign   
## [169] benign    malignant benign    malignant malignant
## Levels: benign malignant

# To get the probabilities and not only the class.
predict(model, validationData, type="raw")

##               benign    malignant
##   [1,]  1.000000e+00 2.385476e-09
##   [2,]  1.000000e+00 4.177284e-10
##   [3,]  1.574442e-11 1.000000e+00
##   [4,]  2.125509e-07 9.999998e-01
##   [5,]  1.000000e+00 2.955862e-10
##   [6,]  1.000000e+00 2.735238e-11
##   [7,]  1.000000e+00 2.735238e-11
##   [8,]  5.018680e-31 1.000000e+00
##   [9,]  1.964288e-18 1.000000e+00
##  [10,]  4.151633e-41 1.000000e+00
##  [11,]  1.805664e-29 1.000000e+00
##  [12,]  7.705031e-29 1.000000e+00
##  [13,]  6.987738e-06 9.999930e-01
##  [14,]  1.558827e-22 1.000000e+00
##  [15,] 2.134333e-228 1.000000e+00
##  [16,] 1.126710e-293 1.000000e+00
##  [17,]  2.308198e-49 1.000000e+00
##  [18,]  9.999687e-01 3.132862e-05
##  [19,] 1.083392e-293 1.000000e+00
##  [20,]  1.000000e+00 1.594460e-10
##  [21,]  1.000000e+00 6.318427e-11
##  [22,]  2.388429e-82 1.000000e+00
##  [23,]  9.980176e-01 1.982354e-03
##  [24,]  5.577250e-44 1.000000e+00
##  [25,]  1.000000e+00 1.035223e-08
##  [26,]  9.998920e-01 1.080034e-04
##  [27,]  1.000000e+00 8.324392e-10
##  [28,]  1.000000e+00 2.186675e-10
##  [29,]  1.000000e+00 1.840414e-09
##  [30,]  1.862199e-86 1.000000e+00
##  [31,]  7.731573e-25 1.000000e+00
##  [32,]  1.000000e+00 4.755188e-09
##  [33,]  1.000000e+00 1.648639e-10
##  [34,]  1.000000e+00 1.099427e-10
##  [35,]  1.000000e+00 5.740503e-10
##  [36,]  1.000000e+00 1.976535e-11
##  [37,]  1.291797e-12 1.000000e+00
##  [38,]  5.452567e-18 1.000000e+00
##  [39,]  1.000000e+00 1.322059e-11
##  [40,]  6.911270e-92 1.000000e+00
##  [41,]  1.000000e+00 1.271146e-09
##  [42,]  8.536396e-68 1.000000e+00
##  [43,]  7.773646e-81 1.000000e+00
##  [44,]  1.000000e+00 2.987490e-10
##  [45,]  1.000000e+00 9.390121e-11
##  [46,]  3.487436e-66 1.000000e+00
##  [47,]  1.000000e+00 2.296086e-09
##  [48,]  1.000000e+00 4.972827e-11
##  [49,]  1.000000e+00 4.971436e-11
##  [50,]  1.000000e+00 6.280840e-11
##  [51,]  1.000000e+00 1.014753e-09
##  [52,] 8.708672e-166 1.000000e+00
##  [53,]  2.001951e-54 1.000000e+00
##  [54,]  6.422500e-69 1.000000e+00
##  [55,]  2.364115e-20 1.000000e+00
##  [56,]  1.094550e-23 1.000000e+00
##  [57,]  9.999991e-01 8.925816e-07
##  [58,]  4.692859e-18 1.000000e+00
##  [59,]  1.000000e+00 1.363163e-09
##  [60,]  1.000000e+00 3.355953e-09
##  [61,]  1.623789e-54 1.000000e+00
##  [62,]  6.035982e-58 1.000000e+00
##  [63,]  9.999996e-01 4.236032e-07
##  [64,]  1.974297e-44 1.000000e+00
##  [65,]  1.000000e+00 4.971436e-11
##  [66,]  2.398156e-36 1.000000e+00
##  [67,]  1.000000e+00 8.032011e-10
##  [68,]  3.158062e-14 1.000000e+00
##  [69,]  9.817653e-01 1.823470e-02
##  [70,]  1.000000e+00 1.351274e-10
##  [71,]  4.410488e-44 1.000000e+00
##  [72,]  0.000000e+00 1.000000e+00
##  [73,]  7.172866e-80 1.000000e+00
##  [74,]  1.000000e+00 4.971436e-11
##  [75,]  1.257713e-10 1.000000e+00
##  [76,]  9.998968e-01 1.031797e-04
##  [77,]  7.951030e-25 1.000000e+00
##  [78,]  1.000000e+00 1.322059e-11
##  [79,]  2.869640e-35 1.000000e+00
##  [80,]  1.000000e+00 4.179689e-09
##  [81,]  1.000000e+00 1.829539e-11
##  [82,]  3.617957e-47 1.000000e+00
##  [83,]  1.000000e+00 1.322059e-11
##  [84,]  1.000000e+00 2.311413e-11
##  [85,]  1.997754e-20 1.000000e+00
##  [86,]  1.545453e-15 1.000000e+00
##  [87,]  1.271787e-15 1.000000e+00
##  [88,] 2.250488e-221 1.000000e+00
##  [89,]  4.294558e-24 1.000000e+00
##  [90,]  0.000000e+00 1.000000e+00
##  [91,]  1.000000e+00 2.735238e-11
##  [92,]  1.000000e+00 2.126838e-10
##  [93,]  1.000000e+00 5.197332e-10
##  [94,]  1.000000e+00 1.322059e-11
##  [95,]  2.677625e-04 9.997322e-01
##  [96,]  1.000000e+00 4.169608e-09
##  [97,]  3.788186e-54 1.000000e+00
##  [98,]  1.000000e+00 6.106006e-10
##  [99,]  1.000000e+00 1.829539e-11
## [100,]  1.532659e-68 1.000000e+00
## [101,]  1.421684e-03 9.985783e-01
## [102,]  1.195370e-58 1.000000e+00
## [103,]  9.999983e-01 1.654438e-06
## [104,]  9.999999e-01 6.511079e-08
## [105,]  7.514335e-87 1.000000e+00
## [106,]  9.999982e-01 1.758357e-06
## [107,]  1.000000e+00 4.755188e-09
## [108,]  1.000000e+00 1.134097e-09
## [109,]  2.838647e-36 1.000000e+00
## [110,]  8.970340e-56 1.000000e+00
## [111,]  1.000000e+00 2.135961e-10
## [112,]  9.999914e-01 8.626064e-06
## [113,]  1.000000e+00 1.322059e-11
## [114,]  1.000000e+00 1.670271e-11
## [115,]  1.000000e+00 2.048484e-09
## [116,]  1.000000e+00 1.575355e-10
## [117,]  4.987931e-77 1.000000e+00
## [118,]  1.000000e+00 3.593459e-11
## [119,]  1.000000e+00 7.944666e-11
## [120,]  1.000000e+00 6.132197e-10
## [121,]  1.000000e+00 1.120644e-09
## [122,]  3.682535e-22 1.000000e+00
## [123,]  9.997819e-01 2.180738e-04
## [124,]  1.000000e+00 1.099427e-10
## [125,]  1.000000e+00 1.933137e-10
## [126,]  1.000000e+00 7.938322e-10
## [127,]  1.000000e+00 1.976535e-11
## [128,]  1.000000e+00 1.322059e-11
## [129,]  1.218724e-67 1.000000e+00
## [130,]  1.000000e+00 2.633891e-10
## [131,]  4.735150e-38 1.000000e+00
## [132,]  6.141877e-32 1.000000e+00
## [133,]  1.000000e+00 1.406247e-09
## [134,]  1.000000e+00 9.663993e-10
## [135,]  1.000000e+00 3.593459e-11
## [136,]  6.190452e-41 1.000000e+00
## [137,]  1.000000e+00 8.032011e-10
## [138,]  1.000000e+00 4.971436e-11
## [139,]  3.058055e-85 1.000000e+00
## [140,]  1.000000e+00 3.380256e-10
## [141,]  1.770307e-69 1.000000e+00
## [142,]  1.694771e-54 1.000000e+00
## [143,]  9.788137e-67 1.000000e+00
## [144,]  1.000000e+00 4.972827e-11
## [145,]  1.000000e+00 1.829539e-11
## [146,]  1.000000e+00 7.394183e-10
## [147,]  9.998429e-01 1.571402e-04
## [148,] 5.864479e-103 1.000000e+00
## [149,]  1.000000e+00 2.135961e-10
## [150,]  9.858815e-35 1.000000e+00
## [151,]  1.000000e+00 2.750252e-10
## [152,]  1.000000e+00 4.972827e-11
## [153,]  5.438479e-29 1.000000e+00
## [154,]  1.000000e+00 8.550687e-10
## [155,]  1.000000e+00 1.768683e-09
## [156,]  9.999999e-01 1.150790e-07
## [157,]  1.000000e+00 1.547702e-08
## [158,]  1.000000e+00 1.976535e-11
## [159,]  1.000000e+00 9.557517e-09
## [160,]  1.000000e+00 7.944666e-11
## [161,]  1.000000e+00 1.705540e-09
## [162,]  1.000000e+00 4.972827e-11
## [163,]  1.000000e+00 5.861203e-10
## [164,]  1.792218e-17 1.000000e+00
## [165,]  1.000000e+00 1.322059e-11
## [166,]  1.000000e+00 1.829539e-11
## [167,]  1.000000e+00 1.322059e-11
## [168,]  1.000000e+00 6.821228e-10
## [169,]  9.999999e-01 5.537676e-08
## [170,] 5.796299e-203 1.000000e+00
## [171,]  1.000000e+00 1.322059e-11
## [172,] 4.009855e-127 1.000000e+00
## [173,]  5.420348e-46 1.000000e+00

Evaluation

To evaluate the model we use the MLmetrics and the ROCR packages.

ytest <- validationData$Class
pred <- predict(model, validationData)
pred_prob <- predict(model, validationData, type="raw")
ConfusionMatrix(pred, ytest)

##            y_pred
## y_true      benign malignant
##   benign        99        10
##   malignant      2        62

Accuracy(pred, ytest)

## [1] 0.9306358

Precision(ytest, pred)

## [1] 0.980198

Recall(ytest, pred)

## [1] 0.9082569

F1_Score(ytest, pred)

## [1] 0.9428571

ROC curves

Given the results of the classifier as probabilities we can calculate the true positive rate (TPR) and the false positive rate (FPR) with the commands:

pred_obj = ROCR::prediction(pred_prob[, 2], ytest, label.ordering=c("benign", "malignant"))
ROCcurve <- performance(pred_obj, "tpr", "fpr")

and we can plot the ROC curve with the commands:

plot(ROCcurve, col = "blue")
abline(0,1, col = "grey")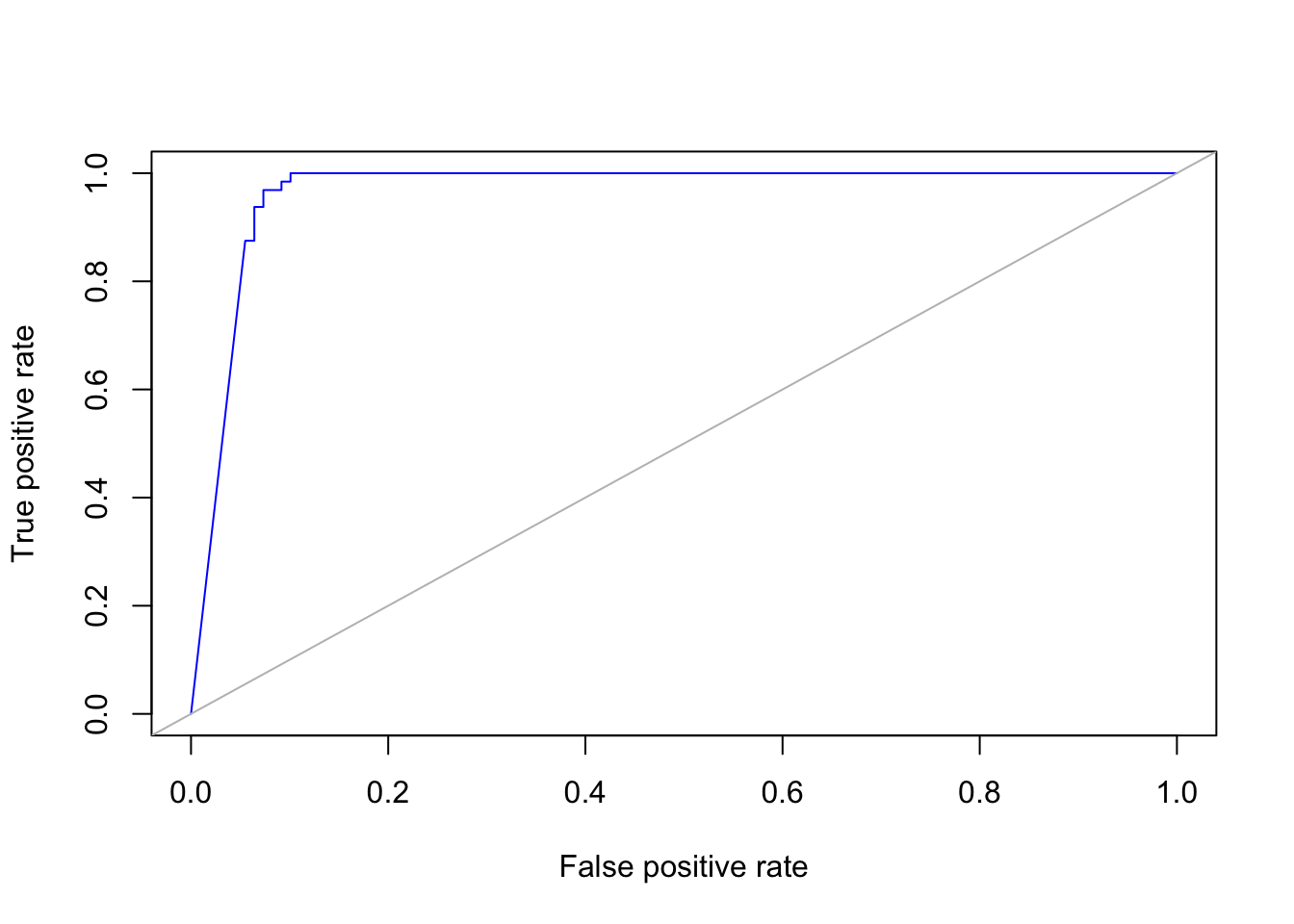

In statistics, a receiver operating characteristic (ROC), or ROC curve, is a graphical plot that illustrates the performance of a binary classifier system as its discrimination threshold is varied. The curve is created by plotting the true positive rate (TPR) against the false positive rate (FPR) at various threshold settings

An ROC curve demonstrates several things:

It shows the tradeoff between sensitivity and specificity (any increase in sensitivity will be accompanied by a decrease in specificity).
The closer the curve follows the left-hand border and then the top border of the ROC space, the more accurate the classifier.
The closer the curve comes to the 45-degree diagonal of the ROC space, the less accurate the test.
The slope of the tangent line at a cutpoint gives the likelihood ratio (LR) for that value of the test.
The area under the curve is a measure of text accuracy. This is discussed further in the next section.

Accuracy is measured by the area under the ROC curve. An area of 1 represents a perfect test; an area of .5 represents a worthless test. A rough guide for classifying the accuracy of a diagnostic test is the traditional academic point system:

.90-1 = excellent (A) .80-.90 = good (B) .70-.80 = fair (C) .60-.70 = poor (D) .50-.60 = fail (F)

Reference: http://gim.unmc.edu/dxtests/ROC1.htm